Methods for heeled resistance estimates (Dec 2013)
Abstract
This article presents the results of calculations for the heeled resistance by two different methods. These results were calculated for two different hull shapes.
The two methods were:
1. The method described in Keuning and Sommenberg (1988) which uses hydrostatic properties of the upright hull. This is called the “Delft Approximation” in the Figures.
2. A method put forward in Fossati (2008) where the hydrostatics of the heeled hull were used with the estimation of residual drag using Keuning (2008). The skin drag was estimated using the method suggested in “Hulls/Drag Measurements on an International One Metre Yacht” from this website.
It is concluded that the topside shape has a significant influence on heeled drag and that unless the topside is similar to that of the Delft models (little if any flare or tumblehome) the second method is likely to be more reliable.
The estimates of drag increase due to heeling were from 0.9% to 4.2% at 2.4 knots and 30 degrees.
1.0 Introduction
 This article compares the results of two different methods of estimating the change in hull drag caused by heeling.
This article compares the results of two different methods of estimating the change in hull drag caused by heeling.
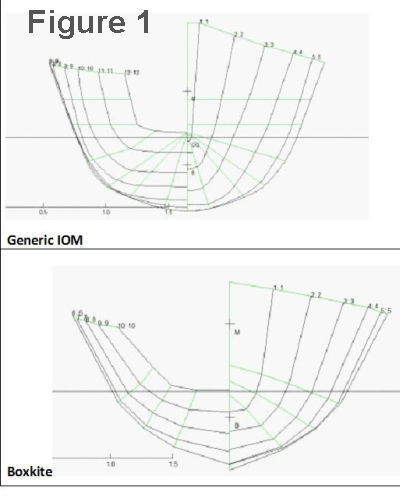
The calculations were done for each of the two different hull shapes as shown in Figure 1.
The first is the generic IOM shape used in the calculations for “Drag Measurements on an International One Metre Yacht” under “Hulls” in this website, which is typical of many middle of the road designs with a narrow transom and only a little flare in the topsides. The other is Boxkite, an old Sails Etc. design by Graham Bantok (used with his permission) which has more flare and a larger transom.
The calculations were done using two methods as follows:
- The method described in Keuning and Sommenberg (1988) which uses hydrostatic properties of the upright hull. This is called the “Delft Approximation” in the Figures.
- A method put forward in Fossati (2008) where the hydrostatics of the heeled hull was used with the estimation of residual drag using Keuning (2008). The skin drag was estimated using the method suggested in “Hulls/Drag Measurements on an International One Metre Yacht” from this website.
2.0 Estimation of changes in wetted surface
The first method (Delft Approximation) estimates the changes in wetted surface as a function of the upright hydrostatics value using the equation in Appendix A1.
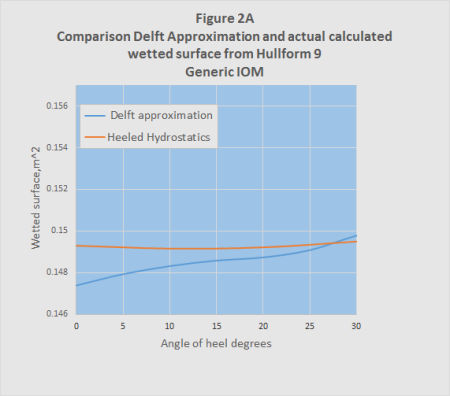
For the second method the wetted surface was calculated using hydrostatics from the hull design program Hullform 9P for different angles of heel.
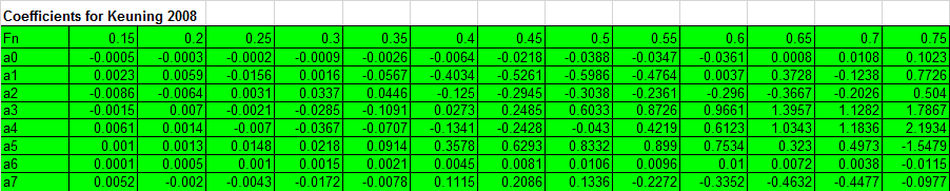
 |
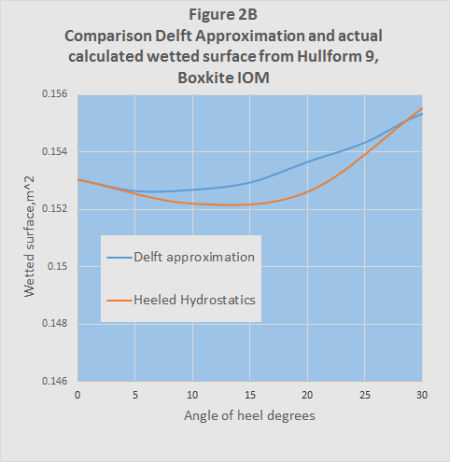 |
Both results are shown in Figures 2A and 2B. It will be seen that although the two methods give answers of the same general order, they do differ significantly. This is not surprising given the large difference between the IOM hull shapes and those used to derive the approximate equations.
3.0 Estimation of changes in residual resistance
The first method, (Delft Approximation) estimates the change in residual resistance at a heel angle of 20 degrees using the equation shown in Appendix A2.
The second method for estimating the residual resistance for various angles of heel was to first calculate the hydrostatic parameters for different heel angles, and then use these parameters in the equation from Keuning (2008) as shown in Appendix A3.
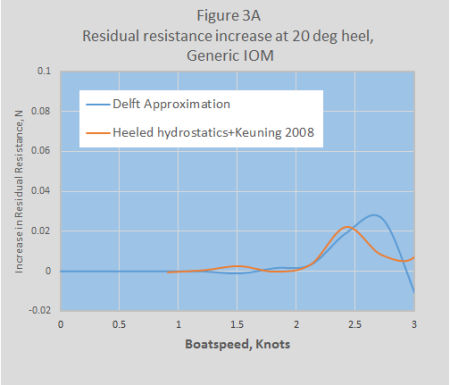
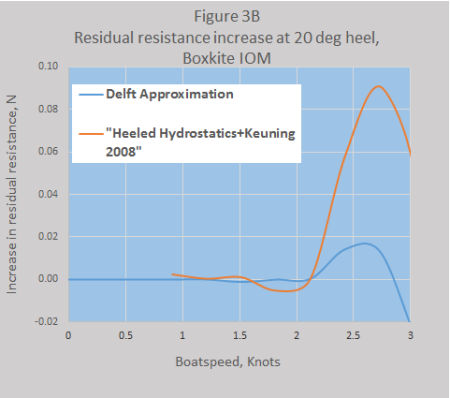
The results for each of the two methods are given in Figures 3A and 3B.
 |
 |
For the Generic IOM the two methods give fairly similar results, though they differ in detail.
For Boxkite, however, the results are very differen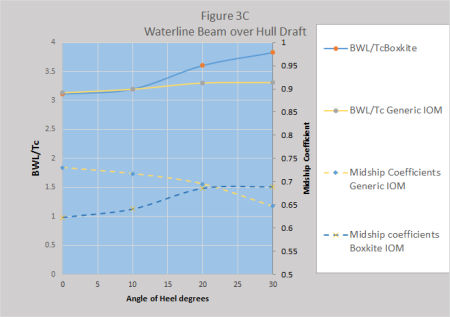 t for speeds above 2 knots. At first the author thought this was just an abberation, however a careful look at the heeled hull parameters showed that two, the midship coefficient and waterline beam over draft, showed not only significantly different values but also a different progression with heel angle between the two hulls.
t for speeds above 2 knots. At first the author thought this was just an abberation, however a careful look at the heeled hull parameters showed that two, the midship coefficient and waterline beam over draft, showed not only significantly different values but also a different progression with heel angle between the two hulls.
Boxkite showed an increasing waterline beam and decreasing hull draft with increasing heel angles. In addition the shape of the midship section as defined by the midship coefficient was also very different for the two hulls. (The midship coefficient is the ratio of the midship area to that of the waterline beam times the draft, so a rectangular section has a coefficient of 1.0 and a triangular one, 0.5). These are compared in Figure 3C.
This "bump" did not show in the Delft approximation because that method does not allow for different topside shapes.
4.0 Estimates of Total Resistance
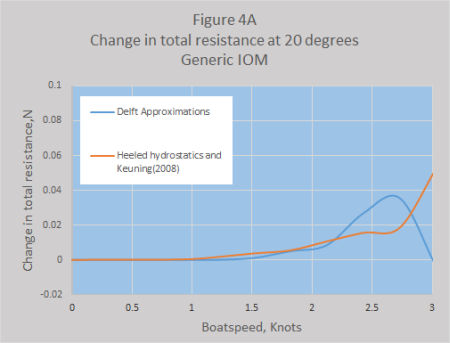
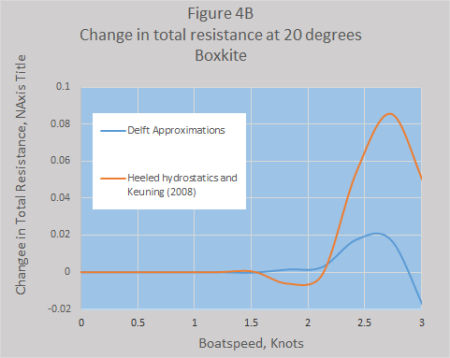
Figure 4A and 4B show the changes in skin resistance plus the changes in residual resistance (i.e.total hull resistance) for each boat for a heel angle of 20 degrees. Once again the two methods are within the same order for the Generic IOM but very different for Boxkite. Going to windward these resistance values are only really applicable at about 2 knots where the total drag on the hull and appendages would be about 1 Newton, and the resistance due to heeling is around 0.6% for the Generic IOM and 0.27% for Boxkite. Higher speeds for this heel angle could probably be obtained when reaching.
 |
 |
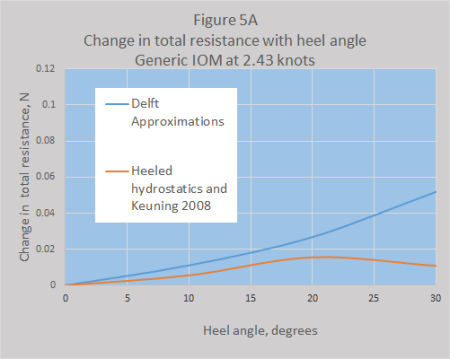
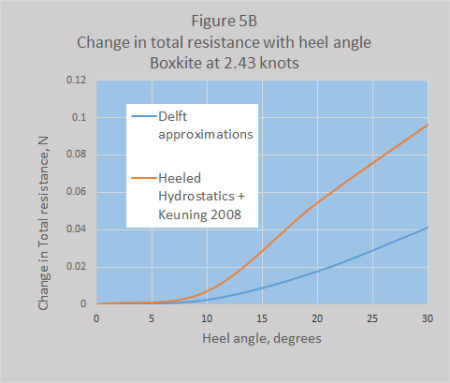
Figures 5A and 5B show the changes in total hull resistance for each boat at a Froude Number of 0.4, equal to 2.43 knots (About the fastest IOM’s go to windward) for a range of heel angles. At this speed the upright hull resistance is just under 2N and, depending on the leeway, the total resistance could be up to around 2.25N. The calculated increase in drag due to heeling at 30 degrees for the Generic IOM was 2.2% for the Delft estimate and 0.9% for that from heeled hydrostatics and Keuning 2008. The comparable figures for Boxkite were 1.8% and 4.2%.
  |
5.0 Comment on Methods
Although the two methods gave, for the most part, answers of the same order, they differed significantly, sometimes one being higher and sometimes the other. Sometimes they even were of different signs. The Delft approximation was proposed for boats of a very different shape than most model yachts with relatively larger beam and displacement for their length and with topsides without significant flare.
If the two methods were used for a velocity prediction program the differences in speeds predicted would be less than 2%, and mostly much lower.
On the whole is probably be safer and more accurate to use the second method i.e. calculating the hydrostatics for different angles of heel and then using these to determine heeled wetted surface to estimate skin resistance and putting the heeled values of hydrostatic parameters into Keuning 2008 to estimate the residual resistance.
The greater increase in heeled resistance for the Boxkite appeared to be the result of the greater flare in the topsides and a wider transom, the difference in drag by this second method at 30 degrees heel and 2.43 knots was 3.3% higher for Boxkite than for the Generic IOM, which is significant and suggests that topside shape needs to be considered carefully in design.
Colin Thorne October 2013
References
Keuning, J.A., and Kargert, M.; A Bare Hull Prediction Method Derived from the results of the Delft Systematic Yacht Hull series extended to higher speeds; International Conf. on Innovation in High Performance Sailing Yachts, Laurient, France, 2008
Fossati, F. Aero-hydrodynamics and the performance of sailing yachts. Allard Coles Nautical London 2009
Keuning,J.A. and Sommenberg,U.B. Approximation of the Hydrodynamic forces on a Sailing Yacht based on the Delft Systematic Series 15th HISWA Symposium Amsterdam, 1988
Appendix A1 Delft Approximation for wetted surface change with heel angle


Appendix A2 Delft Approximation for change in residual resistance


Appendix A3 Keuning (2008) estimate of residual resistance